Introduction
Pathfinding algorithms find a path from point S (start) to point G (goal). The performance of such algorithms depend on the number of iterations in their core loop until a path is found. There are two popular pathfinding algorithms out there, the “Wavefront” and the “A*” (A Star) algorithm. It is my impression that the wavefront algorithm is a bit simpler to understand, whereas the A* algorithm potentially requires fewer iterations. Comparisons between both algorithm can be found in the internet.
This article is about the Wavefront algorithm. It not only describes its principles but also provides a Java Swing demo application which visualizes the progress of a running Wavefront implementation. Lets start with a simple grid. As you can see, we’ve four different markers:
S = Start
G = Goal
0 = free
1 = wall/obstacle
In order to limit the algorithm to the boundary of the grid we put a wall around the grid:
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 0 S 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 G 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
The outer iteration loop of the algorith runs until a path from S to G has been found or no new progression has been made, which means there is no path possible between S and G. The middle iteration loops through the grid either horizontally (row) or vertically (column), and the inner loop will scan through the cells in either the current row or column respectively.
The algorithm is based on the neighborhood connectivity (adjacency) of cells. See the explanation from http://www.cs.tufts.edu/comp/150IR/labs/wavefront.html:
Neighborhood connectivity
There are two ways to connect the cells in a square grid like the one above.
The von Neumann neighborhood of a cell C consists of its 4 neighbors adjacent to the sides of the cell square:
1
4 C 2
3
There are therefore 4 possible moves out of C, and C has 4 children in the graph induced by the von Neumann connectivity.
The Moore neighborhood of a cell C consists of its 8 neighbors adjacent to both the faces and the corners of the cell square:
8 1 2
7 C 3
6 5 4
There are therefore 8 possible moves out of C (including 4 diagnoal moves) and C has 8 children in the graph induced by the Moore connectivity.
The Algorithm
It is important to understand that the algorithm always scans through the entire grid to find the next set of adjacent cells. It does this until a neighboring cell of “G” or previous set of “G” neighbors finally touches the Start cell. Therefore, the outer loop looks like this:
public int autoRun() {
int rc = 0;
try {
while(!wavefrontPass()) {
}
} catch(EndlessLoopException ele) {
rc = 1;
} catch(NoPathFoundException npf) {
rc = 2;
}
return rc;
}
We now decide that the middle loop will loop through each row, so that the inner loop scans through the cells in this row, starting at row 0.
// The instance variable target specifies the next number to mark adjacent cells with.
// Example: If target is 4 (3 corresponds to the goal), this function searches for all cells with target - 1
// and set it to the value of target.
private int target = 3;
public boolean wavefrontPass() throws EndlessLoopException, NoPathFoundException {
boolean found = false;
boolean finished = false;
target++;
if(target > cell.length * cell[0].length) {
throw new EndlessLoopException("An endless loop has been detected. Target value is: " + target);
}
for (int row = 0; row < cell.length; row++) {
for (int col = 0; col < cell[row].length; col++) {
// Only unoccupied cells need to be checked for neighbors
if(cell[row][col] == 0) {
// Watch out for a cell with target - 1 value
int tmpProgress = findNeighbor(row, col, target-1);
if(tmpProgress >= 5) {
// Found the start. Progress indicates the direction where it was found.
// Store cell coordinates which was identified as neighbor of "S".
pos.add(new Dimension(row, col));
finished = true;
}
// At least a neighbor cell was found
if(tmpProgress > 0) {
found = true;
cell[row][col] = target;
// The callback to the simulator applications UI update
if(ui != null) ui.updateTileLabel(row, col, target);
}
}
}
}
if(!found) {
throw new NoPathFoundException("No path can be found. Target value is: " + target);
}
return finished;
}
Take a look at the inner loop. Pay particular attention to the return value of findNeighbor(). They correspond to the four von Neumann neighbors of each cell.
In a 10×10 grid, the inner loop is run exactly 100 times for a single pass. After the first pass, the unoccupied neighboring cells of G (value = 3) have been identified and marked with the value of 4. If at least one free/unoccupied neighbor was found which not also neighbors “S” (start), a new pass of the grid scan is launched. This time, all neighbors of cells marked with a “4” are now marked with a “5”.
The most important functions in the algorithm is to check whether the current cell is a neighbor of the “G” (goal) cell or any previously found neighbor of a neighbor of “G”. See the corresponding code as follows.
private int findNeighbor(int row, int col, int prevTarget) {
int result = 0;
if((row - 1) > 0 && cell[row-1][col] == prevTarget) {
result = 1;
} else if((col + 1) > 0 && cell[row][col+1] == prevTarget) {
result = 2;
} else if((row + 1) < gridSizeX && cell[row+1][col] == prevTarget) {
result = 3;
} else if((col - 1) < gridSizeY && cell[row][col-1] == prevTarget) {
result = 4;
}
// Find out if the next target cell also neighbors the start cell
if(result > 0) {
int x = checkPathFound(row , col);
if(x > 0) {
result = x;
}
}
return result;
}
The findNeighbor functions checks all adjacent cells of the current cell for being one of the prevciously found neighbors or the “G” cell itself. It also calls a function checkPathFound() which checks for the “S” (start) cell. If found, it takes its von Neumann neighbor number and adds 4 to it in order to indicate that this is the final pass. For example, if a neighbor cell was found at the south face of the current cell, findNeighbor stores the von Neumann value 3 in result. Then it checks for the Start cell. If the Start cell is also in the neighborhood, it adds 4 to the current value of 3 so that it finally returns 7:
public int checkPathFound(int row, int col) {
int result = 0;
if(cell[row-1][col] == START) {
result = 7;
} else if(cell[row][col+1] == START) {
result = 8;
} else if(cell[row+1][col] == START) {
result = 5;
} else if(cell[row][col-1] == START) {
result = 6;
}
return result;
}
Of course, you could integrate this function into findNeighbor() but checking for the start cell may also be needed elsewhere.
Examples
Lets take a look at an example. Please note that the goal marker “G” has been replaced with a “3” and the “S” with a “2”. This makes it easier to store integer values in an integer array later. So “3” is our goal. The initial grid looks like this:
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 0 2 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 1 1 1 1 1 1 0 0 0 1
1 0 0 0 1 1 1 1 1 1 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 3 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
As you can see, the example includes a block of walls in the middle.
Note: A couple of months after I wrote this article, I found out that I forgot to mention that the algorithm starts with the goal and make s its way backwards toward the start cell. I forgot why it does that, though.
After the algorithm’s first pass through the grid, it should look like this:
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 0 2 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 1 1 1 1 1 1 0 0 0 1
1 0 0 0 1 1 1 1 1 1 0 4 0 1
1 0 0 0 0 0 0 0 0 0 4 3 4 1
1 0 0 0 0 0 0 0 0 0 0 4 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
In the lower right corner, all four adjacent cells of “3” are now marked with “4”.
The next pass will mark all free cells adjacent to a “4” with a “5”.
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 0 0 1
1 0 2 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 1 1 1 1 1 1 0 5 0 1
1 0 0 0 1 1 1 1 1 1 5 4 5 1
1 0 0 0 0 0 0 0 0 5 4 3 4 1
1 0 0 0 0 0 0 0 0 0 5 4 5 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
Rev. 1.0 of our Wavefront Library
It is good programming practice to seperate program logic from a user interface. In order to adhere to this practice, we will put all the wavefront algorithm logic into its own class file. Nevertheless, for this class to be usefull for our simulator, we implement an interface which requires callback functions in the UI class. These callback methods are used in the algorithm class for letting the UI update itself. If the wavefront algorithm class is not used in an environment that support a UI, for example in a mobile robot, the wavefront class constructor can be called with a null value for the UI class.
package de.psychomechanics;
public interface IUICallback {
void updateTileLabel(int row, int col, int value);
void paintTile(int row, int col, int value);
}
Our WaveFront class will support two modes, single step and auto run. Single step is useful to watch what happens after each pass of the algorithm. See the full listing of the WaveFront class:
package de.psychomechanics;
import java.awt.Dimension;
import java.util.ArrayList;
/**
* The WaveFront algorithm finds a path on a square grid between two coordinates (cells).
* This implementation exposes the following API:
* autoRun()
* wavefrontPass()
* getPath()
*
* @author Stephan Goemans
* @version 1.0
* @since 2017-06-16
*
*/
public class Wavefront {
private final int gridsizeX;
private final int gridsizeY;
private int[][] cell;
private int target;
private int dirChange = 0;
private IUICallback ui;
private ArrayList<Dimension> pos = new ArrayList<Dimension>();
private static int GOAL = 3;
private static int START = 2;
private static int FREE = 0;
private static int WALL = 1;
private static int MARKER1 = 1;
public Wavefront(int[][] cell, IUICallback ui) {
this.cell = cell;
this.ui = ui;
target = GOAL;
this.gridsizeX = cell[0].length;
this.gridsizeY = cell.length;
}
public int autoRun() {
int rc = 0;
try {
while(!wavefrontPass()) {
}
} catch(EndlessLoopException ele) {
rc = 1;
} catch(NoPathFoundException npf) {
rc = 2;
}
return rc;
}
/**
* The instance variable {@code target} specifies the next number to mark adjacent cells with.
* Example: If {@code target} is 4 (3 corresponds to the goal), this function searches for all
* cells with {@code target - 1} and marks it with the value of {@code target}.
*
* @return true if a neighbor of a cell with the previous value of {@code target} was found
*
* @throws EndlessLoopException If the value of {@code target} exceeds the overall number of cells
*
* @throws NoPathFoundException If no path between Start and Goad could be found
*/
public boolean wavefrontPass() throws EndlessLoopException, NoPathFoundException {
boolean found = false;
boolean finished = false;
target++;
if(target > cell.length * cell[0].length) {
throw new EndlessLoopException("An endless loop has been detected. Target value is: " + target);
}
for (int row = 0; row < cell.length; row++) {
for (int col = 0; col < cell[row].length; col++) {
// Only unoccupied cells need to be checked for neighbors
if(cell[row][col] == 0) {
// Watch out for a cell with target - 1 value
int tmpProgress = findNeighbor(row, col, target-1);
if(tmpProgress >= 5) {
// Found the start. Progress indicates the direction where it was found.
// Store cell coordinates which was identified as neighbor of "S".
pos.add(new Dimension(row, col));
finished = true;
}
// At least a neighbor cell was found
if(tmpProgress > 0) {
found = true;
cell[row][col] = target;
// The callback to the simulator applications UI update
if(ui != null) ui.updateTileLabel(row, col, target);
}
}
}
}
if(!found) {
throw new NoPathFoundException("No path can be found. Target value is: " + target);
}
return finished;
}
private int findNeighbor(int row, int col, int prevTarget) {
int result = 0;
if((row - 1) > 0 && cell[row-1][col] == prevTarget) {
result = 1;
} else if((col + 1) < gridsizeX && cell[row][col+1] == prevTarget) {
result = 2;
} else if((row + 1) < gridsizeY && cell[row+1][col] == prevTarget) {
result = 3;
} else if((col - 1) > 0 && cell[row][col-1] == prevTarget) {
result = 4;
}
// Find out if the next target tile also neighbors the car tile
if(result > 0) {
int x = checkPathFound(row , col);
if(x > 0) {
result = x;
}
}
return result;
}
private int checkPathFound(int row, int col) {
int result = 0;
if(cell[row-1][col] == START) {
result = 7;
} else if(cell[row][col+1] == START) {
result = 8;
} else if(cell[row+1][col] == START) {
result = 5;
} else if(cell[row][col-1] == START) {
result = 6;
}
return result;
}
/*
* Follow the path backwards while trying to maintain the same direction
*/
private void recursive(final int row, final int col, final int target, final int direction, final boolean markUICell) {
int ii = 0;
int jj = 0;
if(markUICell) if(ui != null) ui.paintTile(row, col, MARKER1);
// Determine the von Neumann direction ...
switch (direction) {
case 1:
ii = -1;
jj = 0;
break;
case 2:
ii = 0;
jj = 1;
break;
case 3:
ii = 1;
jj = 0;
break;
case 4:
ii = 0;
jj = -1;
break;
}
// ... and check if the next lower number (t-1) can be found in this direction.
if(cell[row+ii][col+jj] == target - 1) {
recursive(row+ii, col+jj, target-1, direction, markUICell);
// If the next lower number could not be found in the stored direction, try all other directions
} else {
dirChange++;
if(cell[row-1][col] == target - 1) {
recursive(row-1, col, target-1, 1, markUICell);
} else if(cell[row][col+1] == target - 1) {
recursive(row, col+1, target-1, 2, markUICell);
} else if(cell[row+1][col] == target - 1) {
recursive(row+1, col, target-1, 3, markUICell);
} else if(cell[row][col-1] == target - 1) {
recursive(row, col-1, target-1, 4, markUICell);
}
}
return;
}
/**
* Returns a List with the sequence of cell coordinates that make up the path between
* Start and Goal
*
* @return ArrayList<Dimension>
*/
public ArrayList<Dimension> getPath() {
int tmpPos = 0;
int tmpDirChanges = Integer.MAX_VALUE;
ArrayList<Dimension> path = new ArrayList<Dimension>();
for(int a=0; a<pos.size(); a++) {
// Find initial direction from goal to first adjacent number
int direction = checkPathFound(pos.get(a).width, pos.get(a).height) - 4;
// Get the number of directional changes
dirChange = 0;
recursive(pos.get(a).width, pos.get(a).height, target, direction, false);
// If smaller than previous paths ...
if(dirChange < tmpDirChanges) {
// Store number ...
tmpDirChanges = dirChange;
// ... and source cell from which the path originates
tmpPos = a;
}
}
//Finally, the optimal path will be marked
recursive(pos.get(tmpPos).width, pos.get(tmpPos).height, target,
checkPathFound(pos.get(tmpPos).width, pos.get(tmpPos).height) - 4, true);
return path;
}
@SuppressWarnings("serial")
class EndlessLoopException extends Exception
{
// Parameterless Constructor
public EndlessLoopException() {}
// Constructor that accepts a message
public EndlessLoopException(String message)
{
super(message);
}
}
@SuppressWarnings("serial")
class NoPathFoundException extends Exception
{
// Parameterless Constructor
public NoPathFoundException() {}
// Constructor that accepts a message
public NoPathFoundException(String message)
{
super(message);
}
}
}
As you can see, the constructor takes a two-dimensional array of integers as its first argument. This array must contain the prepared grid. Since we begin with “G” set to a value of 3, the constructor assumes that target must be 4. Right now, its in the responsibility of the library’s user to pass a valid grid to the constructor, with values of 0, 1, 2, and 3 only. Also there must only be a single value of 2 and of 3 in the array.
In order to seperate the UI from the algorithm’s logic, the wavefront class constructor accepts a reference to a class which implements the IUICallback interface with two callback functions in it. The callback functions are called each time a neighboring cell is found, so the UI can update itself. Alternatively, the reference can be null if there is no UI to update.
The Swing UI
In order to seperate program logic from the UI, we have to maintain two synchronized arrays. For the UI, we have an array of JButtons, which will visualize the wavefront algorithm by simply putting the algorithm’s output into the JButton labels. For this to work, we must translate the returned integer array to the labels of the JButton array in the UI (lines 139 – 148).
When the “New” button is pressed, the grid will be reset and prepopulated with a wall around it. Every tile in the grid can be clicked upon, so it toggles through the values “1” (wall), “2” (Start), “3” (Goal), and ” ” (free).
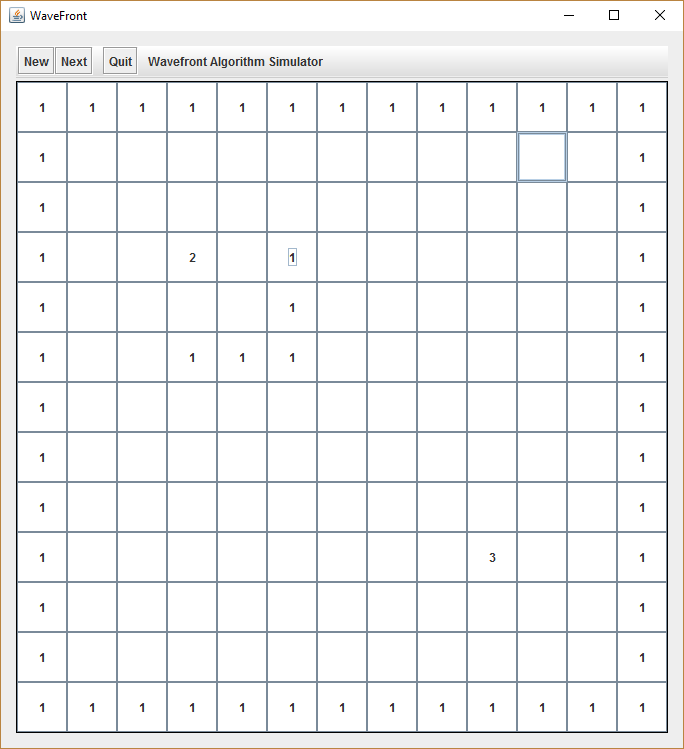
Again, there are two ArrayLists which need to be kept in sync. The JButton ArrayList of the UI and the corresponding integer array (cell) for the algorithm. In our case, the integer values of the returned grid array must be converted into strings for the JButton labels. In addition, the integer value of 0 in the grid array is converted to an empty string for the JButton label.
package de.psychomechanics;
import java.awt.BorderLayout;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.GridLayout;
import java.awt.HeadlessException;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.util.ArrayList;
import javax.swing.JButton;
import javax.swing.JComponent;
import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JOptionPane;
import javax.swing.JPanel;
import javax.swing.JToolBar;
import javax.swing.SwingUtilities;
import javax.swing.border.EmptyBorder;
import javax.swing.border.LineBorder;
import de.psychomechanics.Wavefront.EndlessLoopException;
import de.psychomechanics.Wavefront.NoPathFoundException;
public class WaveFrontSimulator extends JFrame implements IUICallback, ActionListener{
private final JPanel gui = new JPanel(new BorderLayout(3, 3));
private JPanel floorgrid;
private final JLabel message = new JLabel("Wavefront Algorithm Simulator");
private JButton btnNew = new JButton("New");
private JButton btnNext = new JButton("Next");
private JButton btnQuit = new JButton("Quit");
private boolean simStart = false;
private boolean lockFloor = false;
private static final int GRIDSIZEX= 13;
private static final int GRIDSIZEY = 13;
private JButton[][] cell = new JButton[GRIDSIZEX][GRIDSIZEY];
private String GOAL = "3";
private String START = "2";
private String FREE = "";
private String WALL = "1";
private Wavefront wf;
private int[][] grid = new int[GRIDSIZEY][GRIDSIZEX];
WaveFrontSimulator() {
initializeGui();
}
public final void initializeGui() {
// set up the main GUI
gui.setBorder(new EmptyBorder(15, 15, 15, 15));
JToolBar tools = new JToolBar();
tools.setFloatable(false);
gui.add(tools, BorderLayout.PAGE_START);
tools.add(btnNew);
tools.add(btnNext);
tools.addSeparator();
tools.add(btnQuit);
tools.addSeparator();
tools.add(message);
floorgrid = new JPanel(new GridLayout(0, GRIDSIZEX));
floorgrid.setBorder(new LineBorder(Color.BLACK));
gui.add(floorgrid);
btnNew.addActionListener(this);
btnNext.addActionListener(this);
btnQuit.addActionListener(this);
btnNext.setEnabled(false);
// Create the JButton Array which represents the tiles in the floorplan
//
// Insets buttonMargin = new Insets(0,0,0,0);
Dimension d = new Dimension(50, 50);
for (int row = 0; row < cell.length; row++) {
for (int col = 0; col < cell[row].length; col++) {
JButton b = new JButton();
b.addActionListener(this);
cell[row][col] = b;
cell[row][col].setBackground(Color.WHITE);
cell[row][col].setPreferredSize(d);
}
}
// Fill the floorplan with the corresponding JButtons
for (int row = 0; row < GRIDSIZEY; row++) {
for (int col = 0; col < GRIDSIZEX; col++) {
floorgrid.add(cell[row][col]);
}
}
}
public final JComponent getGui() {
return gui;
}
public static void main(String[] args) {
Runnable r = new Runnable() {
@Override
public void run() {
WaveFrontSimulator wf = new WaveFrontSimulator();
JFrame f = new JFrame("WaveFront");
f.add(wf.getGui());
f.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
f.setLocationByPlatform(true);
// Ensures the frame has the minimum required size
// in order display the components within it
f.pack();
// Ensures the minimum size is enforced.
f.setMinimumSize(f.getSize());
f.setVisible(true);
}
};
SwingUtilities.invokeLater(r);
}
@Override
public void actionPerformed(ActionEvent ae) {
JButton j = (JButton) ae.getSource();
if(j.getText().equals("Quit")) {
System.exit(0);
}
if(j.getText().equals("New")) {
resetGrid();
btnNext.setEnabled(true);
simStart = true;
lockFloor = false;
return;
}
if(simStart) {
if(j.getText().equals("Next")) {
if(checkGoalAndCarExists()) {
if(!lockFloor) {
lockFloor = true;
// Create a two-dimensional array which reflects the current state of the grid in the UI.
for (int row = 0; row < GRIDSIZEY; row++) {
for (int col = 0; col < GRIDSIZEX; col++) {
if(cell[row][col].getText().equals("")) {
grid[row][col] = 0;
} else {
grid[row][col] = Integer.parseInt(cell[row][col].getText());
}
}
}
wf = new Wavefront(grid, this);
}
try {
if(!wf.wavefrontPass()) {
} else {
ArrayList<Dimension> path = wf.getPath();
JOptionPane.showMessageDialog(null, "Found!");
}
} catch (HeadlessException | EndlessLoopException | NoPathFoundException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
} else {
JOptionPane.showMessageDialog(null, "Select location for start (2) and goal (3)");
}
}
}
if(simStart && !lockFloor) {
if(j.getText().equals(START)) {
j.setText("3");
} else if(j.getText().equals(WALL)) {
j.setText("2");
} else if(j.getText().equals(FREE)) {
j.setText("1");
} else if(j.getText().equals(GOAL)) {
j.setText("");
}
}
}
private boolean checkGoalAndCarExists() {
boolean car = false;
boolean goal = false;
for (int row = 0; row < cell.length; row++) {
for (int col = 0; col < cell[row].length; col++) {
if(cell[row][col].getText().equals(GOAL)) goal = true;
if(cell[row][col].getText().equals(START)) car = true;
}
}
return(goal && car);
}
private void resetGrid() {
for (int row = 0; row < cell.length; row++) {
for (int col = 0; col < cell[row].length; col++) {
if(col == 0 || row == 0 || col == GRIDSIZEX-1 || row == GRIDSIZEY-1) {
cell[row][col].setText(WALL);
} else {
cell[row][col].setText("");
}
cell[row][col].setName("" + ((row * GRIDSIZEX ) + col));
cell[row][col].setBackground(Color.WHITE);
}
}
}
@Override
public void updateTileLabel(int row, int col, int value) {
cell[row][col].setText(String.valueOf(value));
}
@Override
public void paintTile(int row, int col, int value) {
cell[row][col].setBackground(Color.CYAN);
}
}
For mobile robots: minimize the number of directonal changes
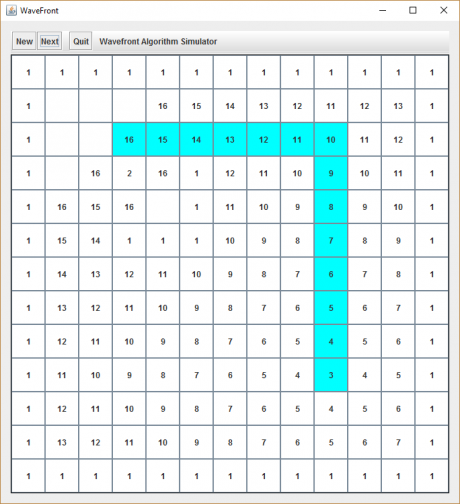
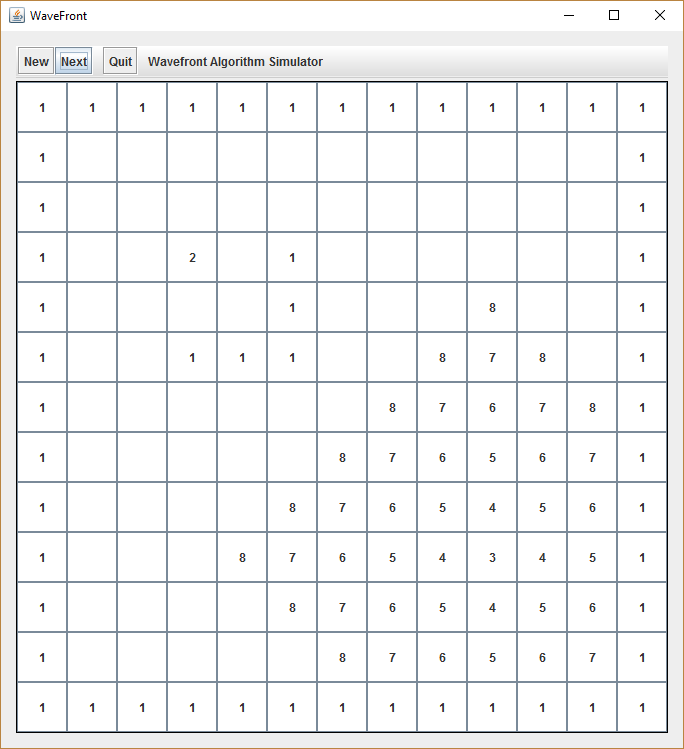
The wavefront algorith is ideally suited to be used by mobile robots. Fortunately, the current version of our wavefront algorith implementation takes into consideration that changing the robots direction by 90 or 180 degrees usually requires a considerable amount of time. At this stage, the algorith prevents slowing down the robot by figuring out the path with the lowest number of directional changes (the ideal path on an empty grid only requires a maximum of one turn, to the left or right). In order to figure out a path with the least directional changes as possible, we need to recursively go back through the cell’s array and follow a decreasing path of stored neighbor numbers while trying to maintain a direction (1 = up, 2 = right, 3 = down, 4 = left). The most complex part of this part of the algorithm is to determine which initial direction to start with at the Start cell (“2”) because, depending on the maze’s complexity, the last pass of the algorith could have touched the Start cell from four different directions. We must store these cell coordinates (pos) to figure out which of these directions will have the least number of turns until reaching the goal.
See the following example, where this situation is about to happen:

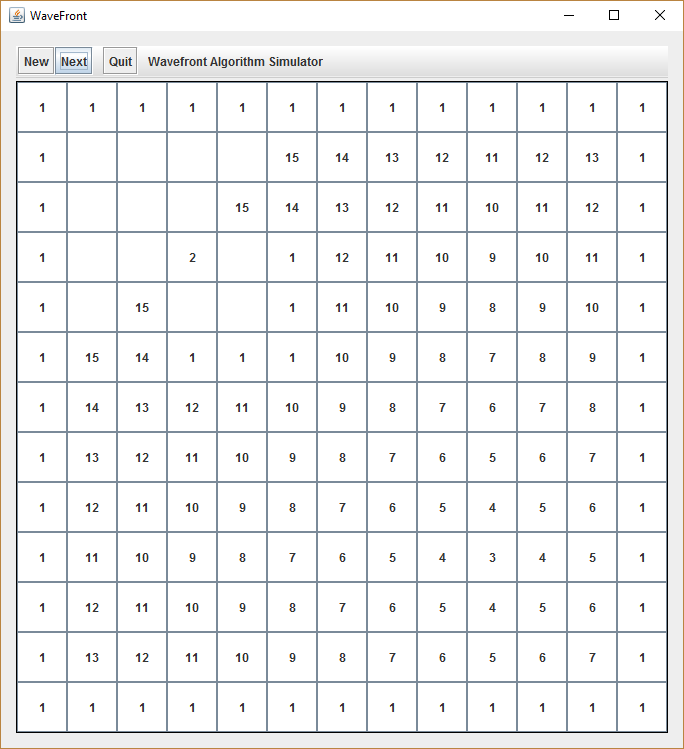
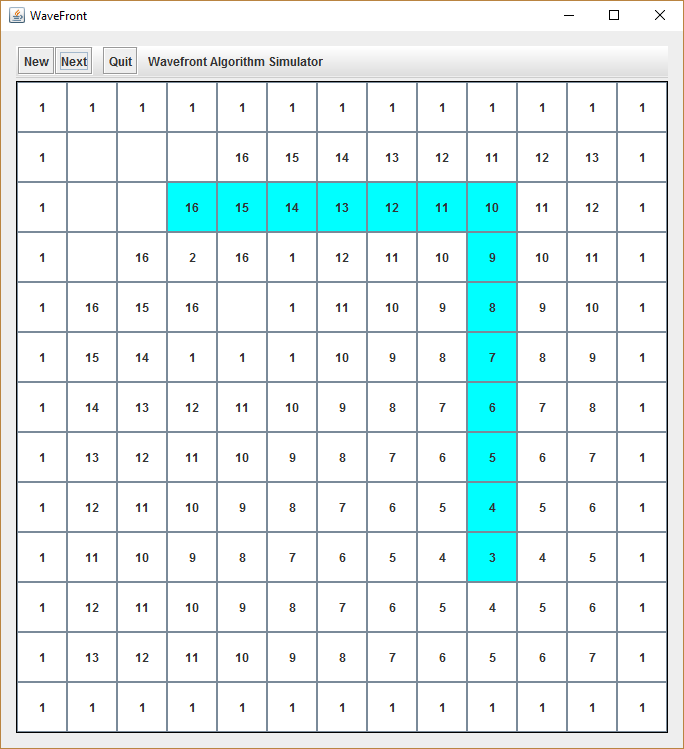
There is still one flaw in our design, and we will not fix it in this article. The path which the function getPath returns, does not take into consideration which direction the robot at “2” looks at when the algorithm finishes.
If you analyze the above situation more deeply, you will recognize that there could be a more efficient path, depending on which direction the robot initially looks at. Let’s assume that the robot faces west, then we would have two turns to reach the goal (left / left). That would also mean it would take him three turns when following the path which is marked in cyan (right / right / right). The situation would reverse if the robot would already be looking north. Then the marked path would be the most efficient one (right / right).